Cutting an equilateral triangle
Here is a problem by Paul Halmos, quoted by Martin Gardner (in Calculus Made Easy by Silvanus P. Thompson and Martin Gardner, 1998):
Cut an equilateral triangle into two parts of equal area by a cut of the shortest possible length. The cut doesn't have to be straight!
Surprising solution.
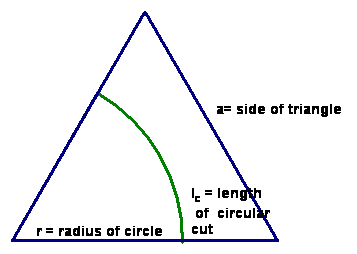
The cut is an arc of a circle!
We will show the proof of this fact at the end of the unit.
First let's compute how much longer a straight cut is than is the circular cut.
The area of an equilateral triangle with side length a, At, is
At = √(3)/4*a2. (You can prove this easily using Heron's formula for the area, or using the usual formula, A = 1/2*b*h.)
And the area of a circle with radius r is
Ac = π*r2.
We want the sector of the circle, Ac/6, to equal one half the area of the triangle, namely, At/2.
So we want Ac/6 = At/2.
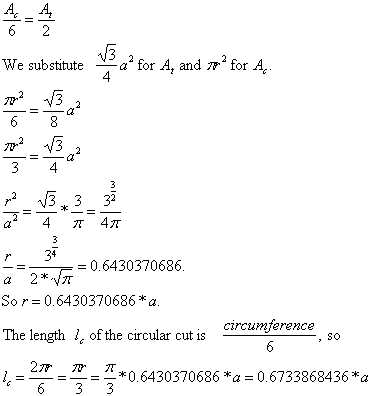
For comparison, the length ls of a straight cut is ls = √(0.5)*a.
(Do you see it? We want the side length of an equilateral triangle with area 1/2 the area of our equilateral triangle with side length a. So the side length will be √(.5)*a, which is 0.7071067812*a.)
ls = .7071067812*a
Thus, ls/lc = 1.0500 ... . So the straight cut is 5% longer.
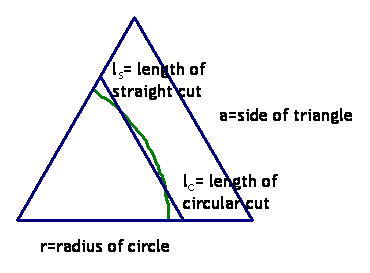
Here we place both cuts on the same triangle:
Proof.
For any shape of a cut that cuts the triangle into two equal areas, take 6 copies of this triangle and arrange them as shown in the picture below.
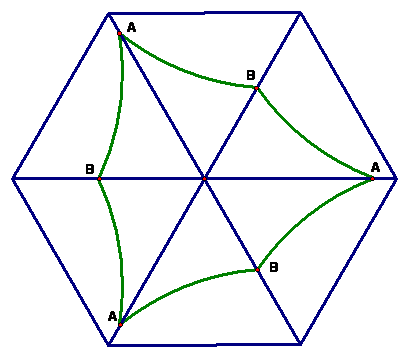
The area of the figure inside the green shape is 1/2 of the area of the hexagon, and its perimeter is 6 times the length of the cut. But the smallest perimeter for a given area is the perimeter of a circle, so the figure inside must be a circle in order to minimize the length of our cut!