Pentágonos Rompecabezas
Introducción
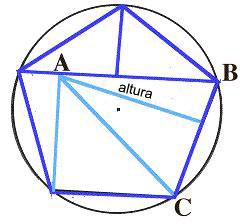
Esta unidad contiene dos actividades relacionadas con la división de pentágonos regulares en triángulos y otros pentágonos menores. Actividad I. [comienzo de página] Un método para calcular el área de un polígono es el dividirlo en triángulos rectángulos, hallando después sus áreas. Por ejemplo, en esta actividad un pentágono regular se puede dividir bien en triángulos rectángulos ó en pentágonos menores. Observe como tales divisiones, con frecuencia, nos proporcionan rompecabezas interesantes. Cómo proceder: Divida un pentágono regular en 6 triángulos rectángulos. Córtelos y habrá obtenido un rompecabezas que podrá reconfigurar de nuevo. 
Materiales: CCompases,
transportadores de ángulos, reglas, tarjetas de índice (o tarjetas
triángulares)
donde dibujar ángulos rectos, cartulina gruesa de colores, papel de
construcción (o embalaje) rígido, tijeras, una calculadora simple y
sobres donde guardar las piezas de rompecabezas. Notas 1. Existen cinco soluciones a este problema. Si los/as estudiantes realizan más de un rompecabezas, éstos deberán ser de distintos colores; de otro modo las piezas se entremezclarían sin remedio. 2. Los/as estudiantes habrán de saber, de antemano, cómo dibujar un pentágono regular. La precisión en tal dibujo y el corte de sus piezas son importantes. Así, el mayor desafío intelectual se halla en el diseño mismo. Si los/as estudiantes no supieran dónde comenzar, el/la maestro/a les puede mostrar una de las soluciones. 3. Observará que los triángulos con las mismas formas (triángulos similares) se usan una y otra vez, por lo que esta lección se puede emparejar con unidades que traten de áreas, similitudes, o incluso estrellas. Soluciones 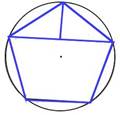 Esta imagen muestra el primer paso a tomar. Un pentágono regular se halla inscrito dentro de un círculo. La parte superior del pentágono está dividida en dos triángulos rectos. Este primer paso es común a todas las soluciones abajo presentadas. Tales soluciones difieren entre sí sólo en la subdivisión del cuadrilátero inferior en 4 triángulos.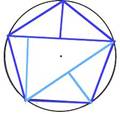 
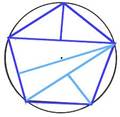
Estas tres últimas soluciones se obtienen a través de dibujar el triángulo ABC con diferentes alturas.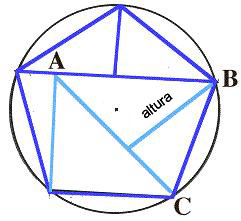 
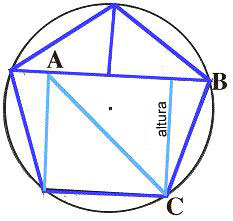
Una variante de esta unidad consiste en dibujar los rompecabezas, pero sin cortarlos. Actividad II. [comienzo de página] Uno puede también crear pentágonos rompecabezas a través de dividir un pentágono regular en 6 pentágonos menores, con áreas iguales. Cómo proceder: Divida un pentágono regular en 6 pentágonos. Córtelos y habrá obtenido un rompecabezas que puede recomponer.
Materiales: Compases, transportadores de ángulos, tarjetas de índice (o
triangulares) para dibujar ángulos
rectos,
cartulina de colores, papel rígido de construcción o de embalar,
tijeras, una calculadora simple y sobres para guardar las piezas de
rompecabezas. 1. Usando papel de construcción rígido, dibuje un pentágono dentro de otro pentágono regular de mayor tamaño. El pentágono central deberá ser también regular (y, por lo tanto, similar al pentágono mayor). 2. Los cinco pentágonos restantes no son regulares. éstos son congruentes entre sí, mienras que sus áreas combinadas repesentan 5/6 del área del pentágono mayor. ¿Se le ocurre una forma de operar? Si no, ívéa abajo! 3. Una vez que haya dividido el pentágono, córtelo en piezas para formar un bonito rompecabezas. Soluciones Inscribimos primero un pentágono regular dentro de un círculo con radio r, y cuya área es 1/6 del área del círculo mayor. (Véa la imagen abajo.)  El área del círculo menor (con radio r) es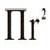 
Por lo tanto,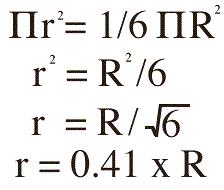 
Así, si el radio R de nuestro círculo mayor es de 10 cms., el radio r del círculo menor será de 4.1 cms. Inscribimos ahora un pentágono regular dentro del círculo menor. En nuestra imagen, sus lados no son paralelos a los lados del pentágono mayor, sino que se hallan rotados en 36° (vea la imagen abajo).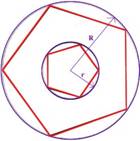 
Ahora, el área que se halla dentro del pentágono mayor y fuera del pentágono menor es 5/6 el área del pentágono mayor. Queremos dividirlo en cinco pentágonos congruentes. ¿Se le ocurre alguna forma de hacerlo? íHay infinidad de maneras! Aquí le mostramos algunos ejemplos de soluciones.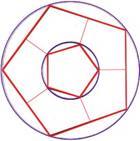 
[índice de lecciones]
Traducción: Miguel A. Piquero-Hidalgo.
23 de Septiembre de 2002.
Revisión: Jenna McClellan 17-10-2018 .
|