Nudo Ancestral

Introducción

Los nudos se hacen con cordón, cinta, cuerda o soga. Los matemáticos dicen que un nudo es simplemente una línea enredada en sí misma.Cuando ata dos cabos de cordón juntos, ese nudo se puede desatar. Si el cordón es muy resbaladizo, podrá desatar el nudo simplemente tirando de los dos cabos de cordón. Así, nudos poco usuales, como el nudo cuadrado ó el nudo de la abuelita (granny), mantienen su rigidez mediante la fricción del cordón. Por ello no pueden atarse nudos, que permanezcan largo tiempo atados, con cordón resbaladizo.

Un caso distinto es cuando los bordes de una cuerda se hallan unidos. La cuerda, en tal caso, forma un lazo. No se puede atar un nudo en tal lazo sin cortar la cuerda. En el dibujo a la izquierda se muestra el nudo más simple en un lazo, que no puede desatarse sin cortar la cuerda.

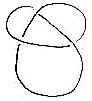
Aunque este nudo de la imagen a la derecha parezca complejo, puede ser desatado, tras lo cual la cuerda podrá recuperar su forma de lazo simple.

Actividad

En esta lección vamos a aprender cómo hacer el antiquísimo nudo aquí mostrado, usando sólo cartulina. Este nudo no tiene ni principio ni fin y, según la tradición popular, representa longevidad e inmortalidad.   Materiales : Tarjetas de índice de 8 " x 5 ", regla, tijeras, pegamento y rotuladores (opcionales).

1. Haga una rejilla con cuadrados de 1/2 "  en el lado rayado de la tarjeta. Dibuje pequeñas marcas a intervalos de 1/2 "  a lo largo de los cuatro bordes de la tarjeta. Dibuje líneas verticales y horizontales en la tarjeta, uniéndo las pequeñas marcas. Así obtendrá una rejilla con 16 "x 10 " = 160 cuadrados, cada uno de 1/2 " cuadrada.

2. Necesitará hacer dos polígonos en la tarjeta, cada uno conteniendo 33 cuadrados. Un polígono es el reflejo del otro. Uno de ellos tiene forma de s con salientes verticales en sus extremos, mientras que el otro tiene forma de una s inversa, también con salientes en sus extremos. Para emparejar ambos polígonos en su rejilla habrá de girar uno de ellos 90 grados. Abajo se muestra el diseño de una de las posibles formas en que los polígonos se pueden trazar.