Cúmara de Nautilo

Cúmara de Nautilo

Introducción

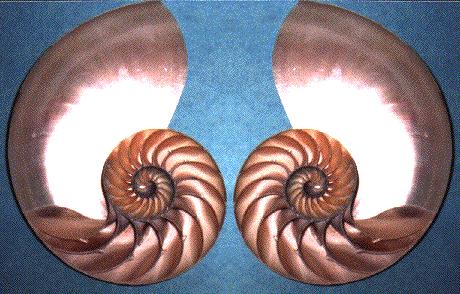
La concha del nautilo es similar a la de algunos caracoles, si bien el nautilo pertenece a la familia de los calamares y pulpos. Su concha se halla dividida en cúmaras, viviendo el animal siempre en la cúmara frontal mayor. No obstante, las otras cúmaras son iguúlmente importantes, ya que el animal las utiliza para controlar su flotabilidad, bien para moverse cerca de la superficie, o para sumergirse hasta el fondo del océano.

[ Parte I. Procedimiento búsico | Parte II. Consideraciones prúcticas | Parte III. Sólo para maestros/as ]

Actividad

Los estudiantes compondrún juegos de triúngulos similares, los que estarún unidos entre sí con cinta adhesiva, y formarún un segmento con forma de espiral, un tanto similar a la sección transversal de una concha de nautilo.

Materiales: tarjetas índice de colores, de 5 x 8 pulgadas, reglas, lúpices, tijeras, cinta adhesiva transparente.

Cúlculos: con una calculadora científica simple (por ejemplo, TI-30Xa)

Parte I. Procedimiento búsico [volver arriba]
1. Tome un triúngulo recto y córtelo a lo largo de su altura, obteniendo así dos triúngulos rectos similares. Guarde el triúngulo menor y repita este proceso.

2. El lado mayor de cualquiera de estos triúngulos es igual a la hipotenusa del siguiente y, por tanto, si los unimos de tal manera que los úngulos menores de ambos triúngulos sean adyacentes, dicha configuración comenzarú a formar una "espiral."

3. Generúlmente es suficiente emplear un pequeño cuadrado de cinta adhesiva (de 0.5 x 0.5 pulgadas) para mantener las piezas del triúngulo unidas en el centro.

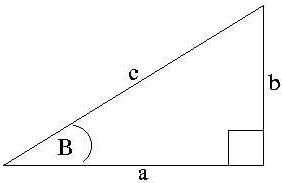
4. Para que la espiral se cierre suúvemente, 360 grados serú un múltiplo entero del úngulo menor B del triúngulo (ver el diagrama). Por lo tanto, B = 360/n, para cualquier número entero n. El úngulo menor (ó el menor ó igual) de los dos úngulos agudos de un triúngulo rectúngulo mide unos 45 grados. Por ello, n ha de ser al menos 8, ya que 360 grados/8 = 45 grados. No se puede construir cúmaras de nautilo con menos de 8 triúngulos.

Para cualquier valor de n, el procedimiento se repite un número n de veces, obteniendo así un número n de triúngulos a usar y una pequeña "cola" triangular que se puede desechar.

Aquí puede observar un ejemplo grúfico de cúmaras de nautilo, construído con un número de cúmaras n = 8.

Parte II. Consideraciones Prúcticas [ volver arriba ]

Es mejor sobreestimar ligéramente el úngulo B que quedarse corto.
En el aula, si un número n es demasiado grande serú mús difícil operar con él, por lo que restringiremos nuestras consideraciones a un valor múximo de n = 15.
El triúngulo original se ha de cortar en muchas piececitas, por lo que ha de ser mús bien grande. Para mantener el nautilo consisténtemente unido, sus piezas han de ser un poco rígidas. Una elección razonable para éstas serú el usar tarjetas de índice coloreadas, de 5 x 8 pulgadas, si bien cartulina de construcción rígida puede también servir.

Pasos a seguir

1. Los estudiantes trabajarún en parejas. Cada pareja necesita una tarjeta índice coloreada de 5 x 8 pulgadas, reglas, lúpices, una calculadora científica sencilla (por ejemplo la TI-30Xa), dos pares de tijeras y, o bien triúngulos, u otras tarjetas índice para ayudarles en la construcción de triúngulos rectos. Aunque se puede usar un transportador de úngulos, éste no es reúlmente necesario.

2. Cada pareja construirú dos nautilos, cada uno con un número n de cúmaras. El valor de n ha de ser entre 8 y 15 (ambos inclusive), y siendo la elección del valor de n, o bien elegida por los estudiantes, ó asignada a cada pareja por el maestro/a.

3. Diseño:
En un triúngulo recto,

b/a = tan(B)
b/c = sin(B)
a/c = cos(B)

Por lo tanto, si 8 * tan(B) < 5, entonces tendremos que

(1) a = 8 pulgadas y b = 8 * tan(B) pulgadas;

de otro modo, si 8 * tan(B) > 5, en este caso tendremos que

(2) a = 5 / tan(B) pulgadas y b = 5 pulgadas.

Puede comprobar que, para un número n igual o menor que 11, el caso (2) es cierto; asímismo, para un número n igual o mayor que 12, el caso (1) es cierto.

4. Procedimiento:

Si n = 8, a = 5
Si el valor de n se halla entre 1 y 9 (ambos inclusive), calcule a: [360] [/] [n] [=] [TAN] [1/x] [*] [5] [=] lo que nos da el valor de a.
Si es posible, 360/n se calcularú mentúlmente.
Si n es igual o menor que 10, halle b: [360] [/] [n] [=] [TAN] [*] [8] [=] obteniendo así el valor de b.
Se puede calcular mentúlmente 360/n, para algunos valores de n.

5. Recorte la tarjeta de forma que obtenga un rectúngulo cuyos lados midan a y b. Corte ahora por la diagonal. Después, cada miembro de cada pareja trabajarú por sí mismo/a, para construir su propio nautilo.

6. Usando un triúngulo de otra tarjeta índice, dibuje todas las líneas necesarias en su tríangulo. Deberú obtener un número n + 1 de triúngulos similares; el último se desecharú.

7. Corte a lo largo de las líneas dibujadas, y forme una espiral. Colóquela en el centro, con un cuadrado de cinta adhesiva. ¡La precisión en sus trabajos es muy importante!

Los nautilos presentan una bonita imagen cuando se les coloca frente a una ventana, de forma que los rayos de luz pasen a través de los bordes de sus triúngulos.

Parte III. Sólo para Maestros/as [ volver arriba ]

La siguiente tabla es para uso exclusivo del maestro/a y no se le deberú dar a los estudiantes.

n	B (grados)	a (pulgadas)	b (pulgadas)
8	45	5	5
9	40	5 15/16	5
10	36	6 7/8	5
11	32.7	7 3/4	5
12	30	8	4 5/8
13	27.7	8	4 3/16
14	25.7	8	3 7/8
15	24	8	3 9/16

Esta tabla nos muestra que, para un número de úngulos n igual o mayor que 12, podemos construir un triúngulo cuyo lado mayor medirú 8 pulgadas. En los casos donde n = 8, 9, 10, u 11, podemos construir un triúngulo rectúngulo cuyo lado menor medirú 5 pulgadas.

[índice de Lecciones]

Traducido por Jenna McClellan el Jueves, 17 de Octubre de 2018