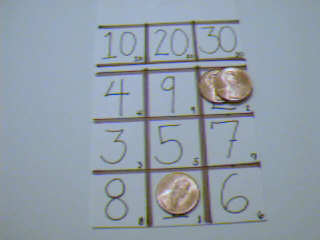Actividad:
Materiales: tarjetas índice de 3" x 5", rotuladores, lápices, y monedas de un centavo (cinco para cada niño/a)

2. Memorizar números a sumar, y ser capaz de recordarlos inmediátamente, es tan importante hoy en día como siempre lo ha sido. No obstante, muchos de los métodos para enseñar a sumar que en el pasado han sido válidos, no son aceptables hoy en día. Uno de tales métodos, que involucraba a la clase entera, funciona como sigue:

El maestro/a nombra dos números, por ejemplo "siete, seis", y apunta hacia un/a estudiante

El/la estudiante se pone en pie inmediátamente, respondiendo "trece", sentándose a continuación.

De esta forma, en pocos minutos, cada estudiante debía responder a dos o tres preguntas, mientras que todos los demás prestaban atención, ya que cualquiera podía ser llamado/a a continuación. Este tipo de "maniobra militar" no se considera aceptable hoy en día, si bien el memorizar, casi automáticamente, el resultado de las sumas de números pequeños requiere bastante práctica, distribuída a lo largo de un periodo prolongado, ésto es algo que resulta bastante aburrido.

3. El cuadrado mágico descrito abajo está diseñado para practicar la suma, lo que se puede realizar con toda la clase, bajo la supervisión del maestro/a.

3.1. Descripción de la Tabla
La tabla es un rectángulo de 3 por 4 1/4 pulgadas, hecho de tarjetas índice de 3 por 5 pulgadas. Esta tarjeta se halla dividida en dos partes: la parte inferior es un cuadrado mágico de 3 por 3, mientras que la parte superior contiene tres números: 10, 20 y 30.

En cada cuadrado el número está inscrito dos veces: Grande y prominente en medio del cuadrado, y al mismo tiempo una pequeña copia de tal número en la esquina inferior derecha, de forma que se pueda leer incluso si se cubre el cuadrado con una moneda de un centavo.

Aquí hallará un ejemplo de un cuadrado de tamaño grande.

3.2. Construyendo la Tabla
Las tablas están pensadas para usarse en grados muy tempranos, desde jardín de infancia hasta segundo, si bien los números han de estar inscritos de forma clara y legible. Iguálmente, la tabla ha de estar construída con una forma atractiva. Cada niño/a en la clase necesita una tabla, por lo que las tablas podrán ser construidas por el maestro/a. O bien, en los grados superiores, se pueden construir las tablas como un proyecto relacionado con el estudio y diseño de los cuadrados mágicos. En tal caso, el uso de tarjetas de índice de colores y de rotuladores, añadirá atractivo a las tablas, individualizando cada proyecto, y convirtiéndose así esta tarea también en un proyecto artístico.

4. Uso de la Tabla
Cada estudiante necesita una tabla (es también útil el uso, por parte del maestro/a, de proyeccion de transparencias). Además, cada estudiante necesita 5 monedas de un centavo, que usará como fichas en la Tabla.

4.1. Posición inicial
Nosotros siempre comenzamos con 2, 3, 4, ó 5 monedas encima del cuadrado mágico. La fila superior se halla iniciálmente vacía. Se pueden apilar dos monedas en un cuadrado, pero SóLO se permite un UN apilamiento de este tipo. Aquí puede observar ejemplos de las 4 posiciones iniciales.

El valor de cada posición es la suma de los números ocupados por las monedas. Dos monedas en la misma posición doblan el valor del número. Por tanto, los valores de los números abajo mostrados son:

4.2. Cálculo
La finalidad de esta actividad es el poder calcular el valor de cualquier posición dada, a través de tomar dos monedas al mismo tiempo, sumando mentálmente los números debajo de ellas. Las decenas se colocan en la fila superior, mientras que las unidades se sitúan de nuevo sobre el cuadrado mágico.

4.3. Reglas
Regla n° 1: Añadir primero dos números de la fila superior. Regla n° 2: Si dos monedas se hallan en el mismo cuadrado, recójalas inmediátamente, doblando el valor del número. Regla n° 3: Si el maestro/a te dice qué monedas has de tomar primero, obedece; si no, puedes optar por recojer dos monedas cualquiera.

5. ActividadesAl principio, el maestro/a explica qué se ha de hacer, usando el proyector. Después dará instrucciones verbales y observará cómo los niños/as trabajan.

La actividad descrita abajo debiera realizarse con frecuencia, durante un corto periodo de tiempo, a un ritmo rápido, aunque sin apurar. Los estudiantes trabajarán individuálmente.

Cada estudiante necesita una tabla de cuadrado mágico, cinco monedas de un centavo, 1 hoja de papel y un lápiz.
(1) Cada niño/a escribe su nombre en la hoja de papel.
(2) El maestro/a les dice la configuración inicial. Por ejemplo: "Dos centavos en cuatro, uno en 6 y uno en 2". Ahora el maestro/a puede decirle a los niños/as qué suma han de realizar primero (por ejemplo, "Sumar 3 y 8 primero"), siempre que ello no contradiga la regla n° 2 arriba expuesta.
(3) Los estudiantes calculan el valor, escribiendo sus respuestas.

Los pasos (2) y (3) se repiten varias veces. Al final, el maestro recoge las hojas con las tareas de los estudiantes.

Notas
(1) Si uno o dos estudiantes se retrasan, dígales que salten al problema siguiente, para no tener a los demás esperando. De otra forma los niños/as pierden su concentración.
(2) Tenga cuidado con los errores aritméticos. Ellos usuálmente indican la existencia de alguna dificultad conceptual.
(3) Si un estudiante comete muchos errores, no le dé ninguna práctica extra hasta que no esté seguro/a de cuál es el problema. De lo contrario, podría reforzar los errores que tal estudiante esté cometiendo.
(4) Tenga cuidado con respuestas tales como 308 (en lugar de 38) ó 105 (en lugar de 15). Tales errores son comunes y se han de corregir de forma inmediata.
(5) Cambie el grado de dificultad, pero no espere, para usar problemas complejos, hasta que los estudiantes dominen los más fáciles.

Algunas notas acerca del número de configuraciones.

[índice de lecciones]