Cometas de Matemáticas

[Nota al lector:

En esta unidad, llamaremos cometas a todos los cuadriláteros. ésta no es la definición general de una cometa. Generálmente, una cometa se describe como un cuadrilátero especial, aunque las definiciones más precisas con frecuencia varían. ésta es la definición general, típicamente usada: Una cometa es un cuadrilátero en el que una de sus diagonales es su eje simétrico. Tal definición equivale a decir que una cometa es un cuadrilátero que tiene dos pares de lados adyacentes que son iguales. Estas dos definiciones incluyen rombos y cuadriláteros no convexos. Hay otras definiciones que son menos inclusivas. Así, a veces sólo se llama cometas a los cuadriláteros convexos, mientras que a los no convexos se les denomina puntas de flechas. Algunas veces se excluye a los rombos por la condición adicional de que no todos los lados tiene la misma longitud.]

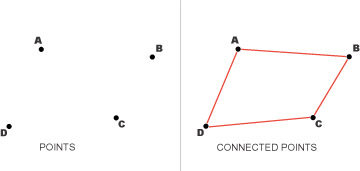
Un cuadrilátero, también llamado cometa, es un polígono de cuatro lados. Para obtener las cuatro esquinas de una cometa, cuatro puntos en el plano han de ser ?independientes.? Esto es, que tres de ellos no yazcan sobre la misma línea recta.

Pero las cuatro esquinas no siempre determinan necesariamente una cometa.

En la figura 1 sólo existe una posible cometa con estas esquinas. Sus lados son:

AB, BC, CD y DA,

y se trata de un polígono convexo.

Figura 1

En la figura 2 existen tres posibles cometas con estas esquinas; sus lados son:

Cometa 1: AD, DB, BC y CA;

Cometa 2: AB, BC, CD y DA;

Cometa 3: AB, BD, DC y CA.

Ninguna de ellas es convexa.

Figura 2

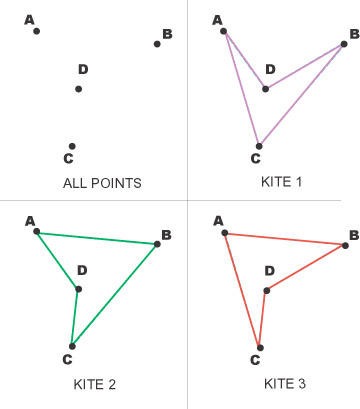
Cada cometa tiene dos diagonales.

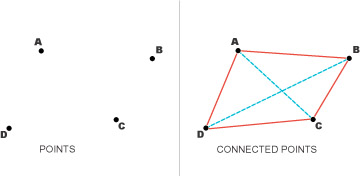		En la figura 3 las diagonales, representadas por la línea de puntos azules, son: AC y BD.
Figura 3
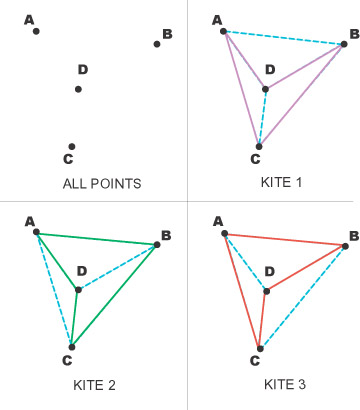		En la figura 4 las diagonales, ambas representadas mediante las líneas de puntos azules son, respectívamente: Cometa 1: AB y CD Cometa 2: AC y BD Cometa 3: AD y BC.
Figura 4

En las cometas convexas sus diagonales se intersectan, mientras que en las cometas cóncavas (no convexas), éstas no se intersectan.

Cada diagonal es menor que 1/2 del perímetro. Por ejemplo, en la figura 3,

|AC| < |AB| + |BC|, and |AC| < |CD| + |DA|,

por una desigualdad de triángulos. Por tanto:

|AC| < ( |AB| + |BC| + |CD| + |DA| )/2.

Además, en cada cometa convexa, la suma de las diagonales es mayor que 1/2 del perímetro. (¿Lo puede demostrar?)

Cada cometa se puede descomponer en dos triángulos. Así, la suma de los ángulos de una cometa es de 360 grados.

Abajo puede observar un gráfico interactivo, que le permitirá explorar algunas de las características de una cometa. En la esquina superior izquierda hay un rectángulo verde. Cuando haga clic en él, el punto D se moverá hacia el punto que usted haya marcado. Si hace clic fuera del triángulo ABC, se formarán tres cometas cóncavas, como se explicó arriba. Note que, en todos los casos, existen cuatro lados y dos diagonales. Puede explorar qué tipo de cometa formarán las diagonales que se cruzan, así como aquellas cuyas diagonales no se cruzan.

Es fácil observar que cada rectángulo forma mosaicos en el plano. Aunque menos obvio, también es cierto el hecho general de que cada pequeña cometa forma mosaicos en el plano. (Algunas de estas configuraciones de mosaicos son muy interesantes.)

Actividad:

Usaremos aquí cometas para formar mosaicos con el plano. Para cubrir el plano, rote cada cometa 180° alrededor del punto medio de cada uno de sus lados. Tales rotaciones llenarán por completo el plano, con copias de la cometa. La figura que se observa arriba es un ejemplo. Imprima y coloree varias cometas idénticas, usando la página para imprimir que se halla más abajo. (¡O diseñe las suyas propias!) Para comenzar, aquí hemos incluído algunas imágenes.

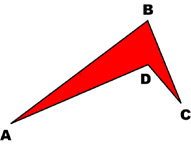	Cometa ABCD
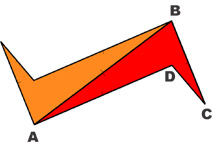	Gire ABCD 180° alrededor del punto medio de AB
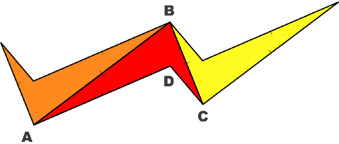	Gire ABCD 180° alrededor del punto medio de BC
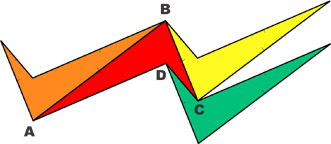	Gire ABCD 180° alrededor del punto medio de CD
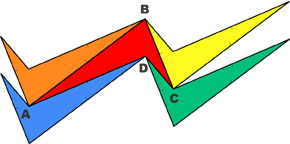	Gire ABCD 180° alrededor del punto medio de AD.

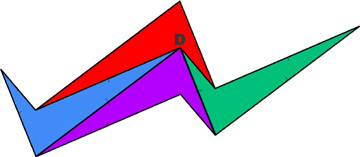
Note que cuatro de los vértices de la cometa siempre se encuentran en un mismo punto. Aquí se muestran cuatro vértices diferentes que se encuentran en el punto D.

COMETAS