Hipérbolas y Elipses
| Introducción A pesar de la popularidad con que gozan las calculadoras gráficas, los/as estudiantes no poseen un buen conocimiento ni de las formas ni de las propiedades de las elipses o las hipérbolas. En la presente unidad los estudiantes aprenderán algunas propiedades básicas de estas curvas, dibujándolas luego para familiarizarse con las mismas. Usaremos la siguiente expresión para elipses e hipérbolas, la cual puede también servir para definirlas. La expresión d(P, Q) señala la distancia entre los puntos P y Q. Una hipérbola es una curva situada en un plano, la cual está determinada por dos puntos, F1 y F2, llamados focos, y un número real c, de forma que 0 < c < d(F1, F2). éste abarca todos los puntos P tales que Una elipse que no sea circular es una curva situada en un plano, la cual también está determinada por dos puntos distintos, F1 y F2, llamados focos, y un número real c, tal que d(F1, F2) < c. éste consiste de todos los puntos P tales que Si mantenemos el valor de c constante, pero desplazamos
F2 hacia F1, hasta que éstos coincidan, las elipses
convergerán en un círculo cuyo centro será F1 y su radio c/2.
ésta es una de las razones por las que el círculo se considera un
caso especial de elipse.
Estas propiedades le permiten dibujar elipses e hipérbolas con considerable precisión, como abajo se muestra. Actividad
Tarea 1: Construyendo una rejilla formada por círculos. Dibuje una línea recta, dividiendo su papel en dos rectángulos de 4 1/4 por 11 pulgadas. Ahora dibuje puntos a lo largo de tal línea, separados un centímetro entre sí (o cualquiera otra unidad de su elección). (Unidades menores nos ofrecen mayor precisión, aunque su uso requiere una tarea más laboriosa.) Numere los puntos, como se muestra en la figura abajo. Elija ahora dos puntos de entre sus focos; por ejemplo, en la figura inferior hemos escogido los puntos n° 8 y n° 19, como nuestros dos puntos focales. Junte ahora su hoja de papel con su cartulina, usando un sujetapapeles. 
Usando un buén compás, dibuje dos grupos de círculos cuyos centros estén situados en F1 y en F2, y que posean radios iguales a los números enteros de su unidad: 1, 2, 3, ... Aquí se muestra una figura con el aspecto que éstos han de tener. Estos círculos forman una rejilla con celdillas de cuatro lados, siendo estos lados no líneas rectas, sino más bien segmentos circulares. 
Note asimismo que las cuatro celdillas se cruzan en cada punto, incluyendo los puntos en los que comenzó, con sólo dos excepciones: las dos celdillas que se cruzan en F1 y en F2. Tarea 2: Dibujando hipérbolas y elipses En cada celdilla, los puntos de una diagonal, sea AD ó BC, se hallan en las mismas hipérbolas, con focos F1 y F2, mientras que los puntos de las otras diagonales se hallan en las mismas elipses (con focos F1 y F2). No obstante, de nuevo hallamos aquí dos excepciones: los puntos situados en la línea que va de F1 a F2, así como una línea perpendicular a ella, yacen en líneas rectas, pero éstos no forman parte ni de una hipérbola ni de una elipse con focos F1 y F2. Prueba. Si tenemos AC y BD situados en dos círculos consecutivos, con el centro en F1, y estando AB y CD situados en dos círculos consecutivos con centro en F2. Si d(F1, D) = r1 y d(F2) = r2, entonces d(F1, B) = r1, d(F1, C) = d(F1, A) = r1 + 1 , y d(F2, C) = r2, d(F2, B) = d(F2, A) = r2 + 1. Por Tanto, d(F1, B) + d(F2, B) = d(F1, C) + d(F2, C) = r1 + r2 + 1 |d(F1, A) - d(F2, A)| = |d(F1, A) - d(F2, A)| = |r1 - r2| Existe una excepción cuando c = r1 + r2 + 1 = d(F1, F2), y también cuando c = |r1 - r2| = 0. Los estudiantes habrán de concluir
sus tareas con el dibujo cuidadoso de varias hipérbolas y de varias
elipses, bien trazándolas a mano libre, o usando una curva Francesa.
Por supuesto, los estudiantes pueden colorearlas en la forma en que
deseen, creando así bellas piezas de arte. Aquí se muestra un ejemplo
de cómo dibujar elipses en esta rejilla (haga clic en la imagen para
verla en su tamaño completo): 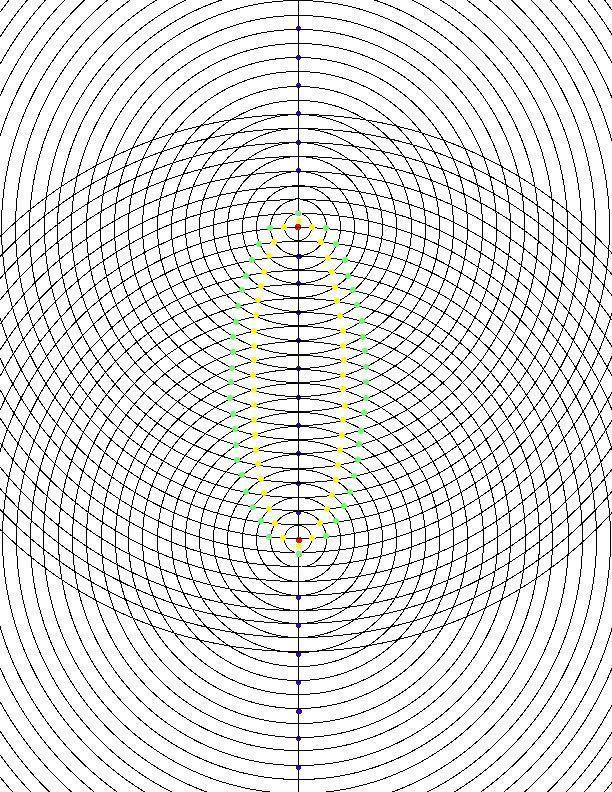
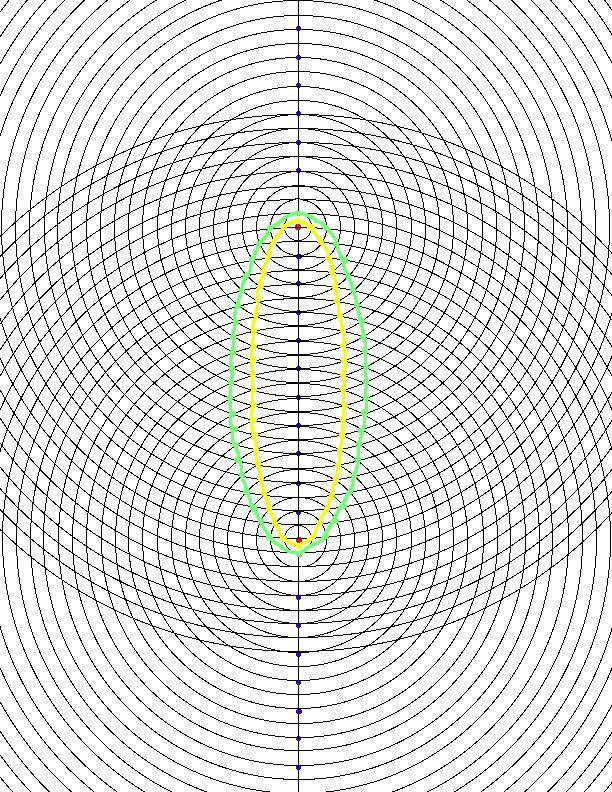
Nota Haga uso de este diagrama para dibujar una hipérbola en esta figura. Aquí puede observar la apariencia del producto final, con dos elipses (una verde y otra amarilla) y una hipérbola (de color violeta). La mayoría de las personas suelen sorprenderse con estos dibujos. Las elipses aparecen más redondeadas de lo que se esperaba, mientras que las hipérbolas aparecen como líneas rectas dobladas ligéramente (lo cual son en realidad). Aquí se muestra, en una figura de primer plano, cómo puede comenzar las elipses y las hipérbolas. 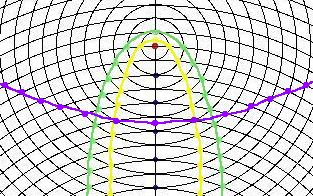
Traducción: Miguel A. Piquero-Hidalgo, 7-Sep.-02
Revisión: Jenna McClellan, 17-10-2018 |