 |
Rompecabezas Circular De Tres Piezas |
 |
 |
Rompecabezas Circular De Tres Piezas |
 |
![]() Materiales:
Materiales:
| Compás |  |
|
Tijeras |
|
| Tarjetas 5" x 8" |
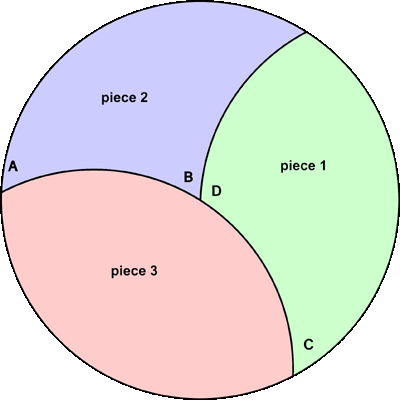
Figura a construir y cortar
 |
Tarea Básica.
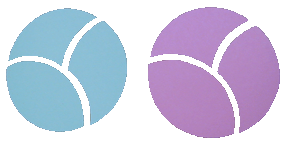 |
|
Figura 1
|
Muéstrele a los estudiantes las piezas del modelo (véa figura 1), e instrúyalos acerca de cómo usar el compás para trazar un círculo grande en una tarjeta índice y luego cortarlo en tres piezas, como se muestra en la figura 1.
Actividades para los grados menores.
(1) Sitúe las piezas formando un círculo.
(2) Forme una figura interesante con las piezas. (Establezca sus propias reglas acerca de qué configuraciones son aceptables.) Una las configuraciones con cinta adhesiva y muéstrelas.
Nota: Existen tantas posibles configuraciones que, en una clase típica, cada estudiante obtendrá algo diferente.
Actividades para los grados superiores.
(1) Hallar el perímetro de cada pieza.
Una solución.
El perímetro de cada pieza es 4 veces 1/6 del
perímetro del círculo inicial. El perímetro de un círculo es 2*![]() *(radio
del círculo). Por tanto, mida el radio y calcule el perímetro de cada pieza.
¡No se olvide de nombrar cada pieza!
*(radio
del círculo). Por tanto, mida el radio y calcule el perímetro de cada pieza.
¡No se olvide de nombrar cada pieza!
(2) Hallar el área de cada pieza.
Una solución.
 |
|
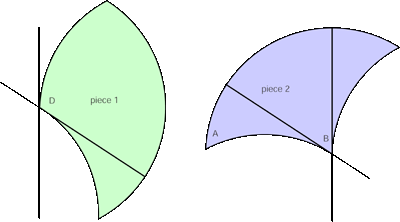
Figura 2
|
Observe la figura 2. Verá que (tras cortar y pegar) la pieza 1 es 1/3 del círculo completo,
ó 1/3 * ![]() *(radio)2, y que la pieza número 2 tiene el área de dos triángulos
equiláteros cuyos lados son iguales al radio del círculo. Por lo tanto tenemos,
*(radio)2, y que la pieza número 2 tiene el área de dos triángulos
equiláteros cuyos lados son iguales al radio del círculo. Por lo tanto tenemos,
área de la pieza 1 = 1/3*
*r2
área de la pieza 2 =
3/2*r2
área de la pieza 3 =
*r2 - las dos previas.
Substituya el valor de r y halle las áreas. No se olvide de nombrar las unidades.
(3) Hallar los ángulos de las esquinas de cada pieza.
Una solución.
El concepto clave aquí es que el ángulo comprendido entre dos líneas curvas es el ángulo comprendido entre las líneas rectas tangentes a ellas, en su punto de intersección. (Vea la figura 3.)
 |
|
Figura 3
|
Comparando la figura 3 con las figuras 2 y 1, se obtiene la conclusión de que
A = B = 60°
C = D = 120°
Revisado por John C. Pierce May 19, 2002
Traducido por Miguel Piquero el 5 de Febrero de 2002
Revisado por Jenna McClellan el jueves, 17 de Octubre de 2018