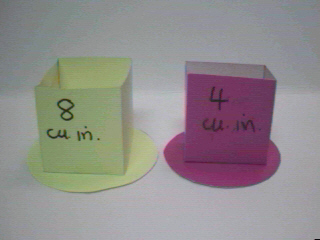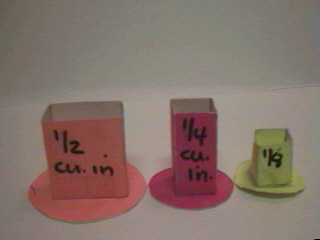Actividad
[ Parte I: Construcción del equipo de medida | Parte II: Uso del equipo ]

Materiales: Papel de construcción o cartulina, tijeras, reglas, lápices, cinta adhesiva.

Parte I. Construcción del equipo de medida [ comienzo de página ]
Los equipos de medidas que vamos a construir consisten en una serie de nueve cajas con capacidades de 1/8, 1/4, 1/2, 1, 2, 4, 8, 16, y 32 pulgadas cúbicas. Abajo se muestran ejemplos de cada una. (Haga clic en cualquier imagen para verla en tamaño grande.)

Estas cajas estan hechas con cartulina, y se apoyan sobre bases circulares relativamente grandes, para que no se vuelquen. Cada caja ha de tener marcada su capacidad, por ejemplo 1/2 pulgada cúbica. (Las etiquetas no tienen que ser exagerádamente visibles, pudiendo colocarse éstas incluso en los fondos de las bases.)

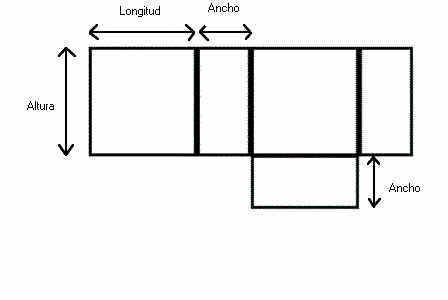
Cada caja se halla abierta en su parte superior. Se usará precisión para su construcción, uniéndolas con cinta adhesiva y pegándolas firmemente a sus bases circulares. Para cajas de tamaño grande, se deberán construir sus bases circulares con cartulina de doble grosor para que no se doble. Es conveniente tener dos de estos juegos en el aula.

Dimensiones de las Cajas

Notas:

• Es preferible tener cajas con aperturas estrechas ya que, con aperturas menores, se reduce el error en las mediciones.
• El diámetro de la base circular se eligió de forma que sea igual a la diagonal mayor de la caja.
• La construcción de las cajas debiera ser un proyecto común de toda la clase. Para ello se puede dividir la clase en 9 equipos, haciendo a cada equipo responsable de dibujar, cortar, ensamblar y etiquetar dos cajas de tamaño distinto.
• Se nombrará a las cajas por su capacidad, de forma que se pueda decir, por ejemplo, "Pásame la de un cuarto."
• La exactitud (teórica) es de 1/16 de pulgada cúbica (la mitad del tamaño de la caja más pequeña).
• La exactitud real es, por supuesto, bastante menor, ya que no se pueden llenar las cajas de forma exacta y total.
• Y, finálmente, se puede obtener cualquier capacidad de entre 0 y 64 pulgadas cúbicas, con bastante aproximación, mediante la combinación de distintos envases (en este caso tendremos 2^9 = 512 valores distintos.)

Nota:
Si usted está familiarizado con la base 2 notará que, tanto las cajas usadas como aquellas omitidas corresponden a unos y ceros, en sus capacidades escritas en base 2:

45 1/2 = 101101.1
18 1/4 = 10010.01
3 5/8 = 11.101

Parte II. Uso del equipo [ comienzo de página ]
El mejor material que puede usarse es probáblemente arroz. Sus granos son pequeños, pero no tan diminutos como para tener que agarrarlos uno a uno, y además no ruedan cuando se derraman.

1. Aprendiendo a medir.

Los niños/as han de aprender a llenar las cajas hasta arriba, sin rebosar y sin tratar de apretar el contenido hacia adentro, lo que originaría que los lados del envase se abultaran. (Las cajas hechas de papel en vez de cartulina gruesa resultan poco útiles.)

Ellos han de aprender a ESTIMAR qué envase han de llenar primero y qué envase han de usar para el grano remanente.

Nota:
Para enseñar estas habilidades se ha de medir dos veces cada cantidad de arroz, por dos estudiantes distintos, o por dos equipos, (preberiblemente con dos juegos de cajas), para detectar cualquier error sistemático que un estudiante pudiera haber cometido en sus mediciones.

El procedimiento básico para medir la capacidad de una jarra es como sigue:

a) Llene la jarra con arroz.
b) Distribuya el arroz entre los envases de forma que

• Todos los envases, excepto el más pequeño que se haya usado, estén llenos con EXACTITUD.
• El envase más pequeño esté más de MEDIO lleno. (Puede hacer una excepción para el envase de 1/8.)

2. Anotando los resultados.

Tras llenar las cajas, los estudiantes calcularán el total mentálmente. (Se puede usar calculadoras, si bien de una forma restringida, ó en casos excepcionales. No obstante, no se harán cálculos con papel y lápiz.)

Nota importante: Es IMPERATIVO el escribir las unidades (pulgadas cúbicas.)

Se pueden usar calculadoras para convertir las fracciones comunes a decimales:

[5] [/] [8] [+] [7] [=] 7.625 (7.6 pulgadas cúbicas).

3. Tareas.
Se puede realizar un elevado número de tareas, ya que el medir es una habilidad práctica, que por tanto requiere de práctica.

4. Organización del aula.
Es importante que TODOS/AS LOS ESTUDIANTES posean una razonable cantidad de práctica. Con el número limitado de juegos de medidas ello representa una tarea consideráblemente difícil. Aquí no sugerimos ninguna solución, aunque recordamos que, ni que el meaestro/a realize demostraciones, ni poniendo a los niños/as a trabajar in grupos grandes, donde algunos niños/as harían las tareas mientras otros tan sólo observarían, NO son sustitutos aceptables de las prácticas personales.

[índice de lecciones]