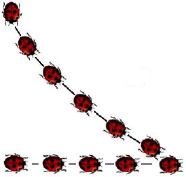
Introducción
Cuando los animales se persiguen entre ellos, lo hacen de formas muy diversas. Así, mientras unos tratan de adelantar a los que persiguen, otros simplemente corren a toda velocidad hacia el animal que persiguen. Ello da lugar a la aparición de un camino curvo si el otro animal tratara de escapar laterálmente. Aquí se muestra un ejemplo.

En esta figura un bichito comienza, en la parte superior, persiguiendo al otro, que trata de escapar hacia la derecha. El camino que toma el primer bichito tiene forma curva.

Problema: Hay cuatro bichitos, situados en las cuatro esquinas de un cuadrado de 15 centímetros de lado.

Los bichitos comienzan a perserguirse uno a otro: 1 persigue a 2 2 persigue a 3 3 persigue a 4 4 persigue a 1

Todos los animales corren con la velocidad de 1 centímetro por segundo

(1 cm/s). ¿Se alcazarán entre sí? ¿Cuándo? ¿Dónde?

Solución: Se encontrarán en el centro del cuadrado en 15 segundos.

Este problema se puede resolver de diversas formas, de acuerdo al nivel de los estudiantes.

Actividad

Materiales: Papel, lápices (de colores, si se desea) y reglas.

1. Escuelas medias y superiores.

Debido a la rotación simétrica, en esta situación los bichitos se hallarán siempre en los cuatro ángulos de un cuadrado, permaneciendo su centro fijo. Ya que un bichito en persecución siempre corre en dirección perpendicular a la dirección de escape, la distancia entre los bichitos decrece en el valor de la velocidad con que corren, esto es 1 cm/s. Por lo tanto, los bichitos se encontrarán en el centro del cuadrado, tras correr durante 15 segundos, recorriendo cada uno una distancia de 15 cms., en una curva espiral hacia el centro.

2. Grados menores.

Para grados menores, el problema debería ser resuelto de forma aproximada, siguiendo el método abajo descrito.

Los problemas con movimiento uniforme se puede resolver, de forma aproximada, a través de dividirlos en intervalos constantes, o cambiando su duración. Con una duración menor para cada intervalo obtendremos una mejor aproximación, aunque es más laborioso.

Comencemos con intervalos de 2 segundos, para después acortarlos a intervalos de 1 segundo, o incluso menos.

La siguiente figura muestra la posición inicial de los bichitos. Haga clic en la imagen para verla en tamaño real.

Aquí se halla una figura grande, que puede imprimir usando la opción PRINT en su navegador. Los bichitos giran y viajan durante dos segundos hacia las nuevas posiciones de sus vecinos, repitiendo el ciclo. Observe qué les ocurre a los bichitos cuando persiguen a sus vecinos.

Conforme los bichitos se aproximan entre sí, los intervalos de tiempo disminuyen. El camino correcto deberá ser más corto que el que se dibuje (de forma que el viaje será también más corto) ya que los bichitos "redondearán las agudas esquinas".

Comentarios

1. Los estudiantes de grados menores deberían usar una hoja de papel de mecanografía con los cuatro puntos ya marcados. La delimitación de los caminos seguidos por los bichitos se ha de hacer con precisión, usando una regla. Al final, después de que los estudiantes hayan dibujado la secuencia de todos los segmentos, habrán de dibujar los bichitos, preferiblemente en los ángulos del cuadrado, coloreando sus trayectorias (las líneas de movimiento de los bichitos). Esto proveerá un elemento de cohesión entre el problema (bichitos persiguiéndose entre sí) y su solución (los caminos que ellos toman). Los estudiantes pueden también dibujar y colorear los cuadrados.

2. Esat unidad se ha enseñado en diferentes grados (incluyendo primero y segundo). Con frecuencia, los maestros instruyen a sus estudiantes a que "conecten los bichitos" con líneas rectas, cada vez que los cuatro bichitos se hayan movido. Ello crea una secuencia de cuadrados que podrán colorearse al final. La figura de abajo, a la izquierda, muestra un dibujo realizado por un/a estudiante de segundo grado, mientras que la figura de la derecha presenta la obra de un estudiante de maestro, aún no graduado. (Haga clic en las figuras para verlas en tamaño grande.)

3. éste es un método poderoso. En su forma analítica (no la gráfica) es la base para resolver sistemas de ecuaciones diferenciales.

4. Este método se puede generalizar a cualquier número de bichitos. A la derecha se muestra el dibujo creado cuando seis bichitos se persiguen entre sí, comenzando en los ángulos de un hexágono regular. Los bichitos pueden viajar con distintas velocidades y comenzar desde una configuración distinta. No obstante, la solución analítica en tal caso se halla más allá de la escuela de matemáticas.