Haga que los estudiantes estimen el volúmen de la caja cúbica ocupado por una pelota que encaje, casi exáctamente, en dicha caja. Anote las estimaciones. (Nuestras estimaciones se situaron entre 2/3 y 4/5.)

b. Peso del arroz necesario para llenar la caja
Llene una caja cúbica con arroz. Si está usando balanzas digitales con la tecla "TARE" podrá colocar la caja vacía, oprimiendo la tecla "TARE," y llenar después la caja con arroz. El peso registrado será entonces sólo el peso del arroz. En nuestro caso, el arroz pesa 550 gramos. Anote tal peso y llámelo X.

c. Peso del arroz necesario para llenar el espacio alrededor de la pelota, cuando ésta se halla dentro de la caja.
Vacíe la caja. Si está usando las balanzas con la tecla "tare," introduzca la pelota dentro de la caja y sitúela encima de la balanza. Presione la tecla "TARE" y en su balanza ahora se leerá cero. Ahora llene el espacio que rodea a la pelota con arroz. ¿Cuánto pesa dicho arroz? En nuestro caso, éste pesó 271 gramos. Anótelo y llámelo Y.

Divida ahora Y entre X; usando una calculadora,
[Y] [/] [X] [%];

Denomine a éste número Z. (En nuestros cálculos tuvimos [271] [/] [550] [%], lo que nos dio un valor para Z = 49.272727, que se puede redondear a 49%.) Hallará que el arroz alrededor de las pelotas tiene un peso aproximado del 50% del arroz contenido en la caja entera.

d. Porcentaje del volúmen de la caja ocupado por la pelota.
Ya que el peso del arroz es proporcional a su volúmen, el arroz ocupa sólo alrededor de un 50% del volúmen de la caja (Z arriba), por tanto la pelota ocupa el volúmen restante, esto es, alrededor del 50% (100 - Z).

Parte II: Solución matemática [volver arriba]

Considere los volúmenes de una esfera y de un cubo:

El volúmen de una esfera de radio r es (4/3)   r3

El volúmen de un cubo cuyo lado sea d es d3

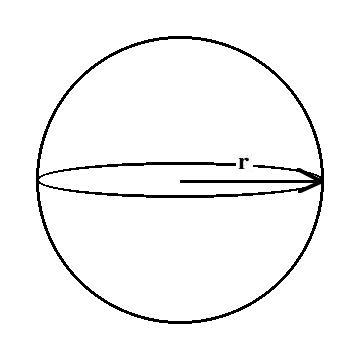
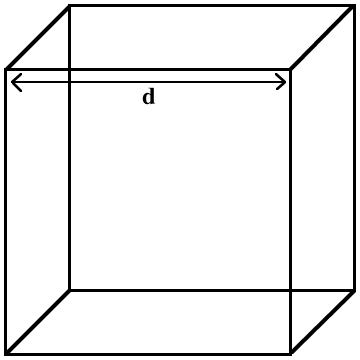
Dado que la longitud del lado de la caja (d) es igual al diámetro de la esfera, d es el doble de la longitud del radio de tal esfera:

D	=	2 x r
d/2	=	r

Substituyendo d/2 por r en la fórmula del volúmen de la esfera tenemos:

volúmen de la esfera	= (4/3) (d/2)3
	= (4/3) d3/8
	= (1/6) d3

Ya que = 3.14159... se halla muy cerca de 3, (1/6) se hallará cerca de 1/2; por tanto, el volúmen de la esfera se puede aproximar a (1/2) d³. Arriba indicamos que el volúmen del cubo es d³. La razón existente entre el volúmen de una esfera y el volúmen de un cubo es:

volúmen de la esfera		(1/2) d3
-----------------------		-----------------------	= 1/2
volúmen del cubo		d3

¡Una esfera que encaje exáctamente en una caja cúbica ocupa alderedor del 50% del volúmen de tal caja (en realidad, un poquito más de la mitad, ya que (1/6) 0.524)!

---

[índice de lecciones]