Introducción
La tabla de sumar es un ingenio que se puede usar para sumar y restar
números decimales positivos de entre 0 y 9999.99, con una exactitud
de 0.1. Su uso requiere tan sólo de la habilidad de saber contar,
sin que haya que contar factores concretos. Por lo tanto, puede ser muy
útil para los estudiantes más jóvenes, como un instrumento
para la solución de problemas. También se puede usar como
herramienta educacional en la enseñanza de la notación decimal,
incluyendo fracciones decimales, así como en la enseñanza
de algoritmos de sumas y restas. Incluso si se usa la tabla sólo
con números enteros, con menos de cuatro dígitos, se recomienda
que dicha tabla sea de tamaño grande.
Aviso: Debido a que la tabla de sumar permite a los niños/as que
realizen sumas y restas para una gran amplitud de números, sin
conocer los factores involucrados en la suma, se ha de tener el cuidado
especial de que los estudiantes practiquen simples sumas mentales (sin
contar siquiera con sus dedos). Queremos enfatizar ésto porque
el perfecto y rápido recuerdo de los factores de la suma se requiere
en tantas situaciones de la vida cotidiana que, cualquier deficiencia
en su conocimiento, puede suponer un serio obstáculo para el futuro
aprendizaje matemático del niño/a.
[Actividades | Otras actividades | Hechos que sus estudiantes deben saber]
Actividad
![]() Materiales:
Tarjetas de índice de 5x8 pulgadas, tijeras, lápices,
reglas, monedas de un centavo u otros objetos pequeños que sirvan
de fichas.
Materiales:
Tarjetas de índice de 5x8 pulgadas, tijeras, lápices,
reglas, monedas de un centavo u otros objetos pequeños que sirvan
de fichas.
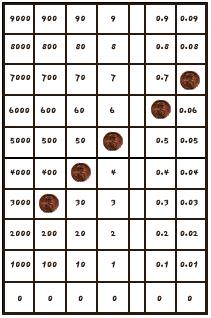
1. Descripción de la tabla y de las fichas: Dibuje 60 cuadrados
de 2 cm x 2 cm, en una tarjeta índice de 5 x 8 pulgadas y numérelas
como se muestra en el diagrama.
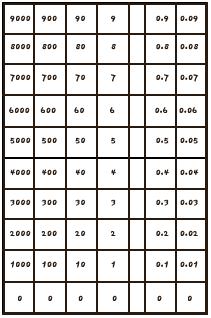
La mayor parte del tiempo no necesitará más de 6 fichas (una por columna). Si bien para otras actividades puede llegar a necesitar hasta 12 fichas (dos por columna). Las monedas de un centavo sirven bien como fichas, pero usted podrá usar tuercas de metal, trocitos de madera, e incluso los cubos Unifix. Es conveniente que las fichas sean pesadas, para que no rueden o vuelquen.
2. Representación de los números: Los números escritos
en notación decimal deberán presentarse en su forma expandida
simple. Por ejemplo,
3450.57 = 3000 + 400 + 50 + 0.5 + 0.07
Se colocan las fichas en los cuadrados numerados con estos números. Así, en este ejemplo tendremos las fichas situadas en los cuadrados [3000], [400], [50], [0.5], and [0.07].
Con frecuencia, se pueden omitir las fichas situadas en cudrados etiquetados con 0, siempre que usted siga las reglas normales para la escritura de decimales:
- Los ceros que preceden al número se omiten mayormente. Por tanto, 12.34 será ráramente escrito como 0012.34, si bien los ceros son a veces convenientes, como cuando se suman columnas de números largos. Por tanto, usted podrá representar dicho número en una tabla de sumar mediante la colocación de fichas en [0], [0], [10], [2], [0.3], y [0.04], ó tan sólo en [10], [2], [0.3], and [0.04], dejando las dos primeras columnas vacias
- También se pueden omitir los ceros situados tras el punto decimal. Por ejemplo,
322.00 = 322.0 = 322
12.30 = 12.3
- No obstante, en el caso de contar dinero, se usarán las normas convencionales. Esto es, si usted representa $5.40 en la tabla, habrá de colocar una ficha en el [0] de la última columna.
- Por otro lado, los ceros situados en medio de un número no se pueden omitir nunca. Por tanto, en el caso de 1200.36, usted ha de colocar fichas en los cuadrados [0] de la 4ª y 5ª columnas.
Para añadir un dígito distinto de cero se procede como sigue:
- Halle la columna a la cual pertenece el número.
- Mueva la ficha en dicha columna hacia arriba, en el número de cuadrados indicados por el dígito.
- Si la ficha se sale de la tabla (de 9 hacia arriba), coloque una ficha en [0], (la ficha saltará abajo), y continúe (hacia arriba).
- Si su ficha no saltó, usted habrá concluído, pero si la ficha saltó, mueva la ficha de la siguiente columna un cuadrado hacia arriba (sumar, o llevarse 1).
- El mover la ficha un cuadrado hacia arriba puede hacerla saltar, si ésta se hallaba en la fila superior. Esto moverá la ficha de la siguiente columna, y así sucesivamente.
|
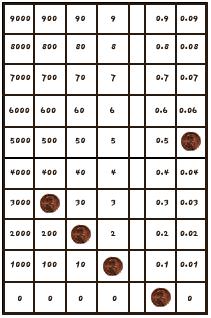
Ejemplo 1: El número 345.67 se representa en la tabla de sumar como aquí se muestra.
|
4. Suma avanzada: En la suma avanzada no se mueven las fichas una a una, contando el número de pasos realizados. Antes bien, usted calcula mentálmente cuál será el cuadrado final donde habrá de mover la ficha. Si la ficha se movió hacia arriba, habrá concluído, pero si la ficha se movió hacia abajo, todavía necesita mover una ficha en la columna situada a la izquierda inmediata un cuadrado hacia arriba (llevándose el resto).
5. Resta: [comienzo de página] Usted siempre
resta un número de otro ya situado en la tabla. El proceso más
básico es el de restar un número de un dígito, distinto
que cero. Así, el restar 503.02 consiste de tres pasos diferenciados:
restar 500, restar 3 y restar 0.02. Tales restas se pueden llevar a cabo
en cualquier orden.
- Halle la columna a la cual pertenece el número.
- Mueva la ficha en dicha columna hacia abajo, en el número de cuadrados indicados por el dígito.
- Si la ficha se sale de la tabla (de 0 hacia abajo), colóquela arriba en [9], (la ficha saltará arriba), y continúe (hacia abajo).
- Si su ficha no saltó, usted habrá concluído, pero si la ficha saltó, mueva la ficha de la siguiente columna a la izquierda un cuadrado hacia abajo (restar, o llevarse 1).
- El mover la ficha un cuadrado hacia abajo puede hacerla saltar, si ésta se hallaba en la fila inferior. Esto moverá la ficha de la siguiente columna abajo, y así sucesivamente.
|
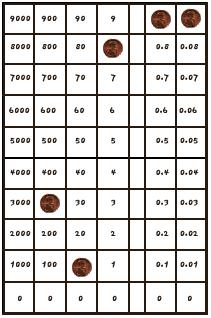
Ejemplo 3: El número 321.05 se representa en la tabla como
|
6. Resta avanzada: En la resta avanzada usted no mueve las fichas una a una, contando el número de pasos realizados. Antes bien, usted calcula, mentálmente, cuál será el cuadrado final donde habrá de mover la ficha. Si la ficha se movió hacia abajo habrá concluído, pero si la ficha se movió hacia arriba, todavía necesita mover una ficha en la columna inmediata, un cuadrado hacia arriba (llevándose el resto).
Otras actividades
[comienzo de página]
1. Construcción de una tabla: El construir una tabla es una actividad
en sí misma, incluso si el esquema se halla ya hecho. El escribir
los números es parte del aprendizaje de la notación decimal
y los estudiantes han de aprender a leer todos los números escritos
en la tabla, ya que éstos son un medio de comunicación.
Por ejemplo, diciendo "pon un centavo sobre un décimo, otro
sobre quinientos y ceros entre medias."
2. Representación numérica: Los estudiantes han de poseer
alguna práctica en la representación de números en
la tabla. Ello consiste de tres pasos, realizados en variados órdenes:
escribir un número, leerlo y colocarlo sobre la tabla. Al mismo
tiempo, los/las estudiantes habrán de aprender la notación
expandida, así como a leerla.
Por ejemplo: 123.4 = 100 + 20 + 3 + 0.4, lo cual se lee , "Ciento veintitrés y cuatro décimos es igual a cien, más veinte, más tres, más cuatro décimos".
Nota: El escribir los números en español puede resultar un ejercicio de deletreo difícil y valioso, el cual provee un interés adicional a este ejercicio, en sí bastante tedioso.
3. Suma y resta básicas: En estas actividades los estudiantes
realizan tres tareas. Por un lado suman (o restan) un número, que
tenga sólo un dígito distinto que cero, a un número
con múltiples dígitos en la tabla de sumar. Luego ellos/as
realizan la misma suma con papel y lápiz, así como con calculadora.
Probáblemente sería mejor si los estudiantes trabajan en
grupos de tres, cada uno usando una de las herramientas enunciadas (tabla,
papel y lápiz, ó calculadora), comparando luego sus resultados.
Dicha actividad requerirá de los estudiantes que éstos memorizen
los hechos de la suma, hasta que dejen de apoyarse en contar cuando mueven
fichas en la tabla.
4. Suma y resta avanzadas: Una vez que los/as estudiantes tengan dominio
sobre los pasos básicos de la suma, así como una competencia
razonable en el uso de los hechos de la suma y de la resta, deberían
intentar la resta entre dos números de múltiples dígitos.
Se les dará los números escritos en la pizarra, de donde
los copiarán, para trabajar con ellos, dígito a dígito.
Una vez que hayan usado un dígito concreto, deberían cruzarlo,
para mantener la cuenta del trabajo ya realizado. Aunque se ha de comprobar
la exactitud de su labor, no creemos que deban usar calculadoras para
tal propósito.
Nota: No evite las fracciones decimales. Los algoritmos son uniformes, por lo que el tratar con decimales no es más complejo que el hacerlo con números enteros.
Hechos
que sus estudiantes deben saber
[comienzo de página]
1. Los algoritmos para sumar y restar possen estructuras muy similares,
si bien sus acciones son opuestas (yendo hacia arriba ó hacia abajo
en la tabla, revierte sus funciones.) Por lo tanto, si usted suma o resta
el mismo número, ambas acciones se cancelan mútuamente.
2. La suma se puede realizar en cualquier orden. Por ejemplo, si usted está sumando 12.34, 56.07 y 8.9, puede colocarlos en la tabla como 10, 6, 0.9 y .07, añadiendo luego el resto como sigue, 8, 0.3, 2, 0.04 y 6.
3. La tabla de sumar es un ingenio de cálculo bastante limitado. En primer lugar, no hay forma de representar los números negativos. Por lo tanto, si trata de restar un número mayor de otro menor se hallará atascado. (El algoritmo requiere que usted mueva una ficha en la siguiente columna a la izquierda, hacia abajo, donde no existe tal ficha.) Para poder usar los números negativos, no sólo se habrá de modificar la tabla, sino también el algoritmo de la resta. Además, el tamaño de los números representados se halla severamente limitado, así como su exactitud (el número de dígitos tras la marca decimal) es pequeño.
Revisado el 13 de Junio de 2002 por John C. Pierce
Traducido por Miguel Piquero el 20/4/2002.