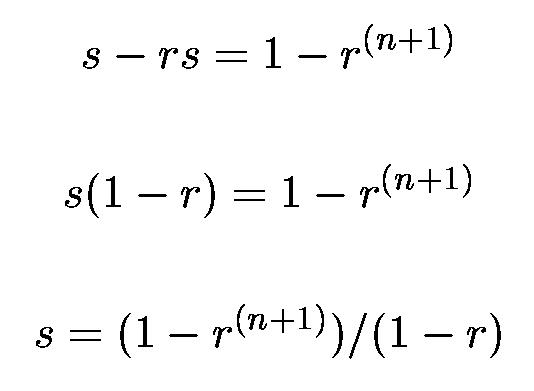
Introducción
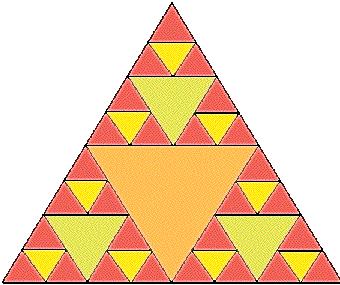
En esta lección aprenderá a hacer triángulos coloridos, también llamados tapetes ó alfombras de Sierpinski, en memoria de W. Sierpinski (1882-1969). Observe aquí como, de la nada, aparece un tapete de Sierpinski, en blanco y negro.
Actividad
![]() Materiales: papel, reglas, rotuladores ó lápices de cera
de colores.
Materiales: papel, reglas, rotuladores ó lápices de cera
de colores.
Instrucciones Básicas:
- Dibujar un triángulo equilátero cuyos lados midan, aproximádamente, 9 pulgadas.
- Unir los puntos medios de estos lados, para formar un triángulo central más pequeño, que tendrá ¼ del área. Píntelo ahora de color verde.
- Unir ahora los tres triángulos delineados, conectándolos a través de los puntos medios de sus lados, y creando así tres triángulos menores. Píntelos de color amarillo.
- Ahora tendrá nueve triángulos coloreados; únalos asimismo a través de los puntos medios de sus lados, obteniendo así nueve triángulos centrales, que coloreará en azul.
- Finálmente, cree 27 triángulos pequeños, en medio de los triángulos sin colorear, y píntelos de color rojo.
- Esta es la apariencia de un tapete de Sierpinski, sin colorear. Puede imprimir este dibujo y decir a sus estudiantes que coloreen los triángulos.
- Aquí puede observar un tapete
de Sierpinski realizado por un estudiante.
- Los verdes ocupan ¼ del área total, quedando otros ¾ .
- Los amarillos cubren ¼ del resto, lo cual es igual a ¼ de ¾, quedando entonces ¾ * ¾ del área total.
- Los de color azul ocupan ¼ de lo que resta, quedando así ¾ * ¾ * ¾ del área total.
- Y los rojos llenan ¼ de los que resta, sobrando ¾ * ¾
* ¾ * ¾ del área total.
Por lo tanto, si continuásemos, cubriríamos
¼ + ( ¼ * ¾) + ( ¼ * (¾)²)
+ ( ¼ * (¾)³) + ... =
¼ * ( 1 + ¾ + (¾)² + (¾)³ + ...
)
lo cual es la suma de una progresión geométrica con el factor ¾ multiplicado por ¼.
2. La suma de esta progresión geométrica es igual a 1/(1 - ¾) = 4 (ver abajo). Por lo tanto, el área cubierta será ¼ * 4 = 1, esto es, el área total. Así, habremos coloreado el área completa, incluso si algunos puntos individuales permanencen en blanco.
Nota: El hecho de comenzar
con un triángulo equilátero se debe tan sólo a motivos
estéticos. Tal resultado será el mismo para cualquier triángulo.
3. Cómo sumar una progresión geómetrica.
|
Digamos que
Entonces, multiplicando por -r,
Sumando las dos ecuaciones de arriba,
|
Traducido por Miguel Piquero: Martes, 22 de Abril de 2002